Lees meer : De Onzekerheid Inherent aan de Kritische Depositiewaarde (KDW): Een Eerst Analyse (een Rapport volgt in 2026). “De Kritische Depositiewaarde (KDW) – Ontstaan, Concept en Praktijk van een Effectgerichte Milieunorm“ Eerder artikel uit 2020 : “Over stikstofgevoeligheid natuur mag je geen vragen stellen”.
In eerdere artikelen op Stikstofinfo.net – zie linkjes bovenaan dit artikel – is de Kritische Depositiewaarde (KDW) ontleed als een historisch gegroeid risicoconcept en is de inherente onzekerheid in de bepaling ervan geanalyseerd . De KDW die in beleid en juridische toetsing wordt gebruikt, is echter één enkel getal geworden.
Maar de wetenschappelijke realiteit achter dat getal is er een van ranges, waarschijnlijkheden en onzekerheidsmarges. De cruciale vraag voor de praktijk is dan ook: hoe groot is die onzekerheid op de KDW precies? Kunnen we deze kwantificeren? In dit artikel duiken we dieper in de statistiek achter de KDW en proberen we een antwoord te geven met behulp van de standaarddeviatie: de meest gebruikte maatstaf voor statistische onzekerheid.
De conclusie is helder: de onzekerheid is substantieel. Een standaarddeviatie van ±2,5 tot ±5 kg N/ha/j is eerder regel dan uitzondering, en zelfs in het meest optimistische scenario is de onvermijdelijke onzekerheid nooit minder dan ±1 kg N/ha/j.
De Empirische Range: Bron van de Standaarddeviatie
De kern van de KDW-bepaling ligt in de zogeheten ‘empirische critical load’ (CLempN), een range die wordt afgeleid uit honderden Europese veldstudies . Deze range, bijvoorbeeld 5-15 kg N/ha/j voor droge heide, vertegenwoordigt de wetenschappelijke onzekerheid. Het is geen exacte waarde, maar een spreiding waarbinnen de ‘echte’ kantelpunt van een ecosysteem waarschijnlijk ligt.
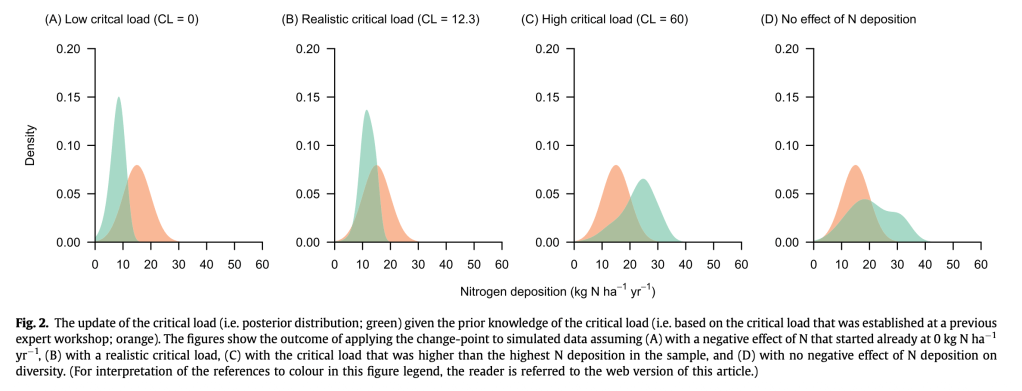
Hoe vertalen we deze range naar een statistische maat zoals de standaarddeviatie (SD)? Een Zwitserse studie van Roth et al. (2017) biedt een directe methode. Zij gebruikten een Bayesiaanse aanpak om KDW’s te schatten en stelden de standaarddeviatie van hun ‘prior’ (de initiële aanname) gelijk aan de helft van de breedte van de empirische range . Deze aanname is logisch: in een normale verdeling ligt ongeveer 68% van de waarden binnen één standaarddeviatie van het gemiddelde. Een range van 10-20 kg (breedte 10 kg) met een gemiddelde van 15 kg impliceert dus een standaarddeviatie van circa 5 kg. Dit is geen losse schatting, maar een directe statistische vertaling van de onzekerheid die door de ecologen zelf is vastgesteld.
Kwantificering van de Onzekerheid per Habitat
Met deze methode kunnen we de onzekerheid voor belangrijke Nederlandse habitattypen kwantificeren, gebaseerd op de officieel gebruikte ranges uit het meest recente KDW-rapport van Wamelink et al. (2023) .
| Habitattype | KDW (kg N) | Empirische Range | Breedte Range | Geschatte Standaarddeviatie (SD) |
| Grijze duinen (kalkarm) | 13 | 5-15 | 10 kg | ± 5,0 kg |
| Droge heiden | 10 | 5-10 | 5 kg | ± 2,5 kg |
| Oude eikenbossen | 15 | 10-15 | 5 kg | ± 2,5 kg |
| Actieve hoogvenen | 7 | 5-10 | 5 kg | ± 2,5 kg |
| Zwak gebufferde vennen | 7 | 5-10 | 5 kg | ± 2,5 kg |
De tabel toont wat de intuïtie al vermoedde: de onzekerheid is groot. Voor de zeer gevoelige droge heiden (KDW 10) is de standaarddeviatie ±2,5 kg. Dit betekent dat er een reële kans is dat de werkelijke kritische grens voor een specifiek heidegebied niet 10, maar bijvoorbeeld 7,5 kg is. Voor de eveneens gevoelige oude eikenbossen (KDW 15) geldt eenzelfde onzekerheid van ±2,5 kg. Voor de grijze duinen, met een bredere empirische range, loopt de standaarddeviatie zelfs op tot ±5 kg.
De Onvermijdelijke Restonzekerheid
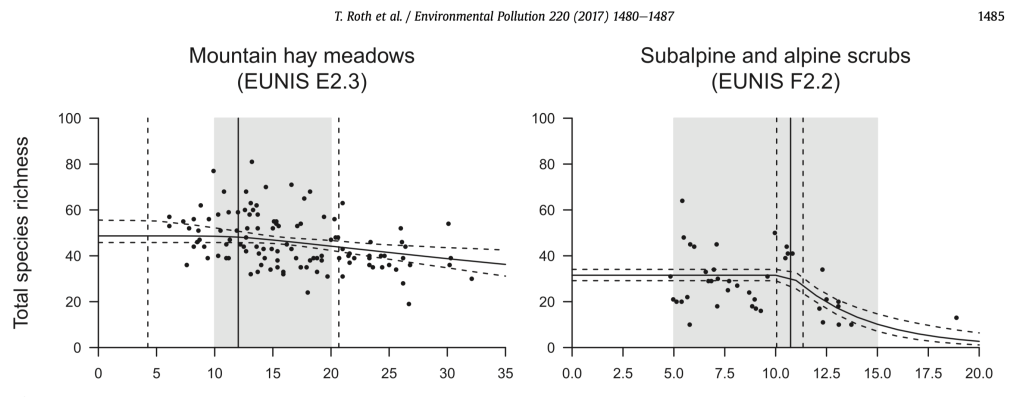
Zelfs met meer data en betere modellen zal de onzekerheid nooit nul worden. De studie van Roth et al. (2017) laat dit goed zien. Voor ‘(sub)alpine scrubs’, een habitattype waarvoor zij over een robuuste dataset beschikten, wisten zij de onzekerheid aanzienlijk te verkleinen. De aanvankelijke (prior) SD was ±5 kg, maar na analyse van de data werd de uiteindelijke (posterior) 95% betrouwbaarheidsinterval slechts 1,2 kg breed. Dit komt neer op een resterende standaarddeviatie van circa ±0,6 kg N/ha/j. Dit kan worden gezien als een ‘best-case’ scenario: onder ideale omstandigheden, met veel data en een duidelijk signaal, blijft er een fundamentele onzekerheid van minimaal ±1 kg over.
Deze restonzekerheid is inherent aan de ecologische complexiteit. Geen twee heidevelden of bossen zijn exact hetzelfde. Variatie in bodemsamenstelling, waterhuishouding, genetische diversiteit, historisch beheer en de aanwezigheid van andere stressfactoren zorgt ervoor dat het kantelpunt altijd een bepaalde spreiding zal hebben.
Van Schijnzekerheid naar Risicomanagement
Het gebruik van één enkel KDW-getal in beleid en vergunningverlening creëert een schijnzekerheid die de wetenschappelijke realiteit niet reflecteert. De onderliggende empirische data tonen een aanzienlijke onzekerheid, die kan worden gekwantificeerd met een standaarddeviatie die voor veel belangrijke natuurtypen oploopt tot ±2,5 à ±5 kg N/ha/j. Dit is geen triviale marge.
Deze constatering pleit niet voor het afschaffen van de KDW, maar voor een andere omgang ermee. In plaats van te focussen op de vraag of een depositiewaarde 0,1 kg boven of onder een enkel getal ligt, zou de discussie moeten gaan over risicomanagement in het licht van deze onzekerheid. Een overschrijding van de KDW is geen binaire constatering, maar een toename van het risico op significant verlies van biodiversiteit. De omvang van de standaarddeviatie geeft aan hoe groot de ‘veiligheidsmarge’ zou moeten zijn als men het voorzorgsprincipe serieus neemt. Het erkennen van een standaarddeviatie van ±5 kg betekent dat een KDW van 15 kg in de praktijk een risicozone van 10 tot 20 kg vertegenwoordigt, een realiteit die het huidige beleid nog onvoldoende erkent.
En laten we eerlijk zijn: wie zich nog druk maakt over 0,0005 mol, 1 mol of zelfs 10 mol. Wie deze getallen even omzet naar kg N, ziet het probleem vanzelf verdwijnen: 0,007 gram, 14 gram of 140 gram stikstof. Dat is geen natuurbelasting, dat is boekhoudkundige fijnslijperij.

Plaats een reactie